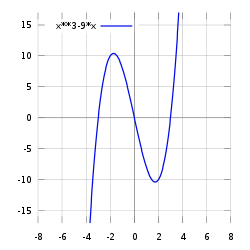
En funktion inom matematiken är en regel som till varje invärde kopplar utvärden. Ofta beskrivs sambandet mellan invärde och utvärde med en matematisk formel, där invärdet representeras med en eller flera variabler, alternativt med en tabell eller grafiskt med en graf, ett sambandsdiagram eller ett pildiagram. En viktig egenskap hos funktioner är att de är deterministiska (det vill säga konsekventa, så att varje invärde alltid ger samma utvärde). Detta gör att funktionen kan ses som en maskin, som systematiskt levererar utvärden så fort man stoppar in invärden.

Invärdet x till funktionen f kallas inom matematisk analys ofta ’’invariabel’’ och inom beräkningsvetenskap för ’’funktionsargument’’ eller ’’argument’’. Det resulterande utvärdet f(x) kallas ’’funktionsvärdet’’ eller ’’värdet’’.

En funktion som är vanligt förekommande som byggsten i matematiska formler kallas elementär funktion, och har ett specifikt namn såsom sinusfunktion, kvadratrot eller logaritm. En funktionsräknare (en vetenskaplig kalkylator) är en miniräknare som kan beräkna värdet av elementära funktioner. En grafritande miniräknare kan visa grafer för funktionsuttryck.

Ordet funktion kommer av latinets functio som betyder "fullgörande, verkställande", det vill säga att någonting görs färdigt, att någonting fixas.^[1]

En funktion är en regel eller procedur som tillordnar ett utvärde för varje givet invärde.^[2] Följande är exempel på funktioner:

• I en grupp människor har varje person en favoritfärg bland färgerna röd, orange, gul, grön, blå, indigo och violett. Invärdet till funktionen är i detta fall en person, och utvärdet är en av de sju färgerna. Favoritfärgen är en funktion av person till färg. Johan kan till exempel ha favoritfärgen röd, medan Kent har favoritfärgen violett. Det är fullt möjligt för två personer att ha samma favoritfärg. Det kan till exempel vara så att både Anna och Johan tycker om rött.

• En sten som släpps från olika våningsplan i en hög byggnad får olika falltid. Det kan till exempel ta 2 sekunder att falla från den 2:a våningen och 4 sekunder från den 8:e. Här är våningsplansnumret invärde och utvärdet är den tid som det tar för stenen att nå fram till markplanet.

Låt A och B vara två mängder, där ingen av dem är tom. En funktion f från A till B är en avbildning från A till B som definierar exakt ett element i B till varje element i A, vilket formellt skrivs f:A → B.^[3]

Normalt skriver man dock f(a)=b där b är det unika elementet i B som f tillordnar elementet a i A. Om det finns minst ett element a för varje element i B kallas funktionen surjektiv.^[4] Om det för varje element i B finns som mest ett element a kallas funktionen injektiv. En funktion som är både injektiv och surjektiv – det vill säga det finns ett och endast ett element a för varje element i B – kallas bijektiv. Bijektiva funktioner är intressanta då de har en invers.

En typ av funktion som ofta diskuteras har matematiska tal både som invärde och som utvärde och fungerar så att utvärdet uttrycks som en formel där (det obestämda) invärdet ingår. Utvärdet beräknas då genom att man först ersätter symbolen för invärdet med ett visst invärde som man är intresserad av. Därefter kan man beräkna ett utvärde för detta invärde genom att räkna ut värdet av den formel som nu innehåller endast kända matematiska tal.

Tänk till exempel på formeln

${\displaystyle f(x)=x^{2}}$

som för varje tal x tillordnar detta tal ett associerat värde, x i kvadrat.

En naturlig generalisering är att låta funktionen bero av flera invärden.^[2] Som exempel är

${\displaystyle g(x,y)=xy}$

en funktion som tar två värden, x och y, och tillordnar dem ett utvärde som är produkten av dem, x . y. Man kan kanske tycka att den här regeln inte stämmer på beskrivningen ovan, eftersom den kräver två invärden. Dock är det fullt möjligt att se varje sådant par av värden som ett enda värde, i vid bemärkelse. Sådana värden kallas ordnade par, (x, y).

I naturvetenskap stöter man ofta på funktioner som inte kan definieras med hjälp av en känd formel. (Det vill säga att man inte känner till någon formel, även om det kanske finns en.) Ett exempel på detta är jordytans temperatur över tiden. Den är en funktion som har plats (två koordinater) och tid som invärde och ger ett utvärde som är en temperatur.

Det intuitiva funktionsbegreppet är alltså inte begränsat till beräkningar från enstaka tal och inte ens begränsat till beräkningar. Det matematiska funktionsbegreppet är ännu mer generellt (obegränsat) och inte alls begränsat till att handla om matematiska tal. Detta gör att funktionsbegreppet är en grundsten i nästan varje gren av matematiken och naturvetenskapen.

Om en variabel y definieras som funktionsvärdet, det vill säga

${\displaystyle y=f(x)}$,

kallas y för beroende variabel, medan x är oberoende variabel.

En funktion^[3]

${\displaystyle f:X\to Y}$

är en binär relation R på X × Y sådan att

${\displaystyle \forall x\in X\ \exists y\in Y(R(x,y)\land \forall z\in Y(R(x,z)\rightarrow z=y))}$

En vanlig beteckning är då

${\displaystyle f(x)=y}$

Om vi frångår ovanstående villkor heter det att funktionen är flervärd. Detta är fallet för många komplexa funktioner, till exempel komplexa logaritm- och argumentfunktionerna och komplex exponentiering med godtycklig bas. Ofta definierar man då en ny funktion som inte är flervärd, och använder den kanoniska principalgrenen av värdena för ett argument. Principalvarianten av en flervärd funktion brukar betecknas med versal i början, till exempel

${\displaystyle \mathrm {Log} ,\,\mathrm {Arg} }$

• Linjär funktion
• Polynomfunktion
• Exponentialfunktion
• Trigonometrisk funktion
• Hyperbolisk funktion
• Gammafunktionen
• Betafunktionen
• Matrisfunktion

• Elementär funktion
• Kontinuerlig funktion
• Glatt funktion
• Analytisk funktion
• Implicit funktion
• Invers funktion
• Sammansatt funktion

• Lista över funktioner
• Derivata
• Integral
• Transformation
• Avbildning
• Operator
• Distribution
• Injektiv funktion
• Surjektiv funktion
• Bijektiv funktion

• Wikimedia Commons har media som rör funktion.