

Digitalteknik är ett område inom både elektroniken och datavetenskapen som handlar om analys och konstruktion av digitala nät. Det vill säga signalbehandling med endast två tillgängliga tillstånd: hög och låg, eller 1 och 0. Digital teknik brukar förknippas med mikroprocessorer och datorer men omfattar även diskreta digitala kretsar, exempelvis ALU (Arithmetic Logic Unit), skiftregister och räknare, som numera är integrerade i ett enda chip. Ämnet tar upp både den abstrakta beskrivningen av nätet och den fysiska realiseringen. Tekniken blir bara mer och mer populär på grund av det låga priset och den systematiska konstruktionen.
Historia
Claude Shannon var den första att formellt tillämpa den booleska algebran inom datavetenskapen. I sin magisteravhandling A Symbolic Analysis of Relay and Switching Circuits från 1937 visade han hur boolesk algebra och binär aritmetik kan användas för att förenkla telefonväxlarnas relänät. Han visade även det omvända, att elektriska nät med brytare kan användas för att lösa booleska problem. Detta blev en av principerna för modern digitalteknik men var egentligen inte helt nytt. Liknande idéer hade använts tidigare, om än mer informellt. Som exempel på tidiga programmerbara maskiner med binärt arbetssätt kan här tysken Konrad Zuses flyttalsbaserade datorer från 1936 (och framåt) nämnas, men det fanns binära automater av olika slag långt tidigare. I sitt vidare arbete med informationsteori använde och generaliserade Shannon flera viktiga resultat av den äldre svensk-amerikanen Harry Nyquist, bland annat samplingsteoremet.
Popularitet
Ett par anledningar till att tekniken blivit och fortsätter bli mer populär
- Lågt pris. Till skillnad från vid analog elektronisk konstruktion så sjunker priset på digitala komponenter för närvarande hela tiden. När tillverkningstekniken förfinas blir kretsarna mindre, strömsnålare och billigare. Kretsarna konstrueras nu för tiden av kisel, vilket är en billig råvara. De flesta nät kan byggas helt av standardkomponenter.
- Systematisk konstruktion. Processen för att konstruera digitala nät har en tydlig struktur och vissa steg går därför att automatisera med hjälp av datorverktyg. Överskådligheten underlättar också planeringen av konstruktionsprojektet och kan hjälpa till att minska antalet buggar.
Teori

Centralt inom digitaltekniken är begreppet funktion, att ett invärde kan sammankopplas med ett bestämt absolutvärde. I den digitala världen är funktionerna binära: indata och utdata kan anta ett av två möjliga värden. Dessa två lägen kallas för hög/låg, 1/0 eller sant/falskt. Detta gör att teori från både logik och boolesk algebra kan tillämpas.
Den enklaste digitala komponenten är en inverterare. Den har endast en ingång och en utgång. Allt den gör är att invertera insignalen, från hög till låg eller vice versa. Inverteraren tillhör de enklaste digitala komponenterna som kallas grindar. Grindar är konstruerade av transistorer och har en, två eller ibland flera ingångar och oftast en utgång. Utvärdet beror på insignalernas värden och på grindens logiska funktion.
De enklaste grindarna är logiska AND ("och"), OR ("eller") och XOR ("exklusivt eller") samt inverterade varianter av dessa: NAND ("inte och", ibland kallad noch), NOR ("inte eller") samt XNOR ("båda eller ingen"). NAND och NOR är de enda två av dessa grindar som själva kan realisera alla typer av logiska funktioner.
Dessa logiska grindar kan sedan kombineras i större nät, och sedan länge tillverkas så kallade mikrochip med inbyggda funktioner enligt en tabell. Ett sådant mikrochip innehåller vanligen 14 in/utgångar eller fler. Vilka som är ingångar resp utgångar måste man slå upp i mikrochipets manual. Två av in/utgånarna används för drivspänning, resten kan till exempel vara 4 NAND-grindar (som enkelt kan göras om till AND-grindar). Eller så kan mikrochipet innehålla 2 NAND- och 2 NOR-grindar. Mer avancerade chip kan innehålla fler än två ingångar samt flera utgångar för varje grind. Med stora system av "grind-chips" kan man tillverka allt från miniräknare till datorer (eller huvuddelarna av datorerna, som processorer, minnen och stora delar av moderkorten. Grindar är, som nämnts, i grunden transistorer. Transistorer kan idag göras mikroskopiskt små. Från slutet av 1960-talet fanns en empirisk formel vars huvudtes var att antalet transistorer på (avancerade) microchip skulle fördubblas på samma yta var 18:e månad. Denna förutsägelse höll i över 30 år, men under 00-talet började konstruktörerna få problem med att elektroner "hoppade över" mellan transistorer. De senaste 10 årens utveckling av till exempel processorer för PC-datorer har därför fått ske med hjälp av "smartare" chip.
Digitala nät kan i huvudsak beskrivas som antingen kombinatoriska nät eller sekvensnät.
Kombinatoriskt nät

Ett kombinatoriskt nät utför en boolesk funktion. Varje kombination på ingångarna har en given utdata på utgångarna. Den booleska funktionen kan beskrivas på flera sätt:
- Sanningstabell. En lista med alla möjliga ingångsvärden visar vad utsignalen kommer att vara vid denna kombination.
- Booleskt uttryck. Ex: , där är en utgång och osv är ingångar. står för logisk disjunktion (ELLER) medan står för logisk konjunktion (OCH).
- Karnaughdiagram. Används för att optimera funktionen och uttrycka den på ett minimalt sätt. Detta ger ett nytt booleskt uttryck.
- Venndiagram
Sekvensnät

Ett sekvensnäts utgångsvärde beror inte bara på indata, utan även i vilken ordning datan kommer (dess sekvens). Ett sekvensnät tar hänsyn både till de nuvarande värdena på ingångarna och dess efterföljande värden. Därför består ett sekvensnät av ett kombinatoriskt nät och ett minne som återkopplas till nätet. Minnet lagrar vilket tillstånd som sekvensnätet befinner sig i, och är i form av ett antal vippor, till exempel D-vippor. Sekvensnätets uppgift är att läsa av det nuvarande tillståndet och insignaler, för att sedan avgöra vilket nästa tillstånd ska vara. Ett sekvensnät är den digitala formen av en tillståndsmaskin och analyseras på samma sätt. Ett sekvensnät är därför antingen av Moore-typ eller Mealy-typ.
Realiseringar
I slutet av konstruktionen byggs nätet upp med logiska grindar och vippor. Kombinatoriska nät kan även realiseras som nät med strömbrytare. FPGA är också ett praktiskt sätt att implementera ett eller flera sekvensnät eller kombinatoriska nät på ett enda chipp. För att kunna programmera en sådan krets används ett hårdvarubeskrivande språk, där de vanligaste är VHDL och Verilog.
Grindteknik
Detta avsnitt behandlar tänkbara realiseringar av alla typer av grindar. Realiseringarna är av pedagogiska skäl gjorda med bipolära transistorer. Moderna digitala kretsar innehåller dock mest MOSFET:s (Metal Oxide Sermiconductor Field Effect Transistor).
Transistorn

Bipolära transistorer finns i två komplementära varianter: NPN-typ och PNP-typ, som skiljs åt genom att strömmarna går åt direkt motsatt riktning. PNP-transistorn används sällan i digitala grindar så vi nöjer oss med att visa NPN-varianten. Transistorn består av tre ben. Dessa är Bas (B), Kollektor (C) och Emitter (E). När transistorn tillförs en ström på basen får man en i regel mycket högre ström på kollektorn. Denna förstärkningsfaktor kallas för Beta (Ic är alltså Beta gånger större än Ib). Beta varierar med både kollektorström, kollektor-emitterspänning och temperatur så den är långt ifrån konstant men brukar för små signaler anses vara konstant. I digitala sammanhang är man dock mest intresserad av dess switchegenskaper; det vill säga vad som krävs för AV (strypt) eller PÅ (bottnad). Därmed får betafaktorn en underordnad betydelse. För småsignaltransistorer kan man räkna med en betafaktor på mer än 100, som betraktas som en tämligen stor betafaktor. Någonting som är bra att tänka på är att en transistor av kiseltyp behöver som minst cirka 0.7 V över bas-emittersträckan för att överhuvudtaget kunna leda någon ström. Denna gräns kallas tröskelspänning.
NOT-grinden (inverterare)

Den enklaste formen av grind är en inverterare. Vi skickar alltså in en signal (x) och får inversen (x') ut. Detta beror på att vi i det höga fallet förser den med så pass mycket basström att transistorn bottnar (0). Från transistoravsnittet ovan har vi ju att räkna med en betafaktor på mer än 100 vilket innebär att det hade räckt med 100k på ingången för att få transistorn att bottna. När vi sedan skickar in en låg signal får transistorn ingen ström alls varvid den blir strypt (1). Valet av 1k kollektormotstånd ger en kanske onödigt hög ström (5mA) vid låg utnivå men det har mest valts av pedagogiska skäl. Både sanningstabellen och grindsymbolen visas till höger.
Av kuriosaskäl kan nämnas att vald realisering av inverterare inte kommer att vara överdrivet snabb. Detta beror på Miller-effekten dvs den multiplicering av kapacitansen mellan kollektor och bas (Cbc) som sker när man har stor förstärkning hos en transkonduktiv komponent. Om författaren minns rätt så kan denna överskottsladdning ledas bort med hjälp av en diod mellan bas och kollektor. Ett annat sätt att snabba på switchningen är en liten kondensator över basmotståndet. Men vi är inte intresserade av snabba datorer här.
NAND-grinden

NAND-grinden är låg när alla ingångar är höga men hög annars. Ingångstransistorerna är kopplade på ett lite speciellt sätt. De får sin basström från det gemensamma basmotståndet på 10k. Så fort minst en av ingångarna går låg så får vi de facto en kortslutning av bas-emittersträckan hos utgångstransistorn. Utgångstransistorn stryps då och vi får hög signal ut. Både sanningstabell och grindsymbol syns till höger.
OR-grinden

OR-grinden är hög när minst en av ingångarna är höga och låg annars. Både sanningstabell och grindsymbol syns till höger. Symbolen >1 är inte helt riktig då det borde vara >=1 (för man kan se ingångarna som en binär summering) men det blir rittekniskt klumpigt.
AND-grinden

AND-grinden är hög när alla ingångarna är höga och låg annars. Vi har här valt att helt enkelt hänga på en inverterare av ovanstående typ. Detta är med andra ord ingen direkt fundamental grind för den kan byggas av de andra tre ovan. Både sanningstabell och grindsymbol syns till höger.
NOR-grinden

NOR-grinden är hög när alla ingångarna är låga och låg annars. Vi har här valt att helt enkelt hänga på en inverterare av ovanstående typ. Detta är med andra ord ingen direkt fundamental grind för den kan byggas av de andra tre ovan. Både sanningstabell och grindsymbol syns till höger. Det finns ett antal flera NOR-grindar, detta är bara en av alla.
XOR-grinden

XOR-grinden är hög när ena ingången är hög (och den andra låg) och låg annars. Vi har här valt att realisera grinden med redan befintliga grindar enligt ovan. Det vore lite spännande att se en diskret version. Man kan naturligtvis även här hänga på en inverterare. Man får då en så kallad XNOR-grind (som indikerar likhet). Både sanningstabell och grindsymbol syns till höger.
Three-state-grinden

En three-state-grind, något oegentligt kallad grind, är, liksom inverteraren, hög när ingången är låg och vice versa (signalen OE måste dock i det här fallet vara hög). För att realisera en icke-inverterande three-state-grind kan man helt enkelt montera en inverterare före grinden. Båda typerna har ett tredje tillstånd dvs högimpediv (OE=0). I detta tillstånd kan man applicera en signal direkt på utgången. Detta krävs när man har att göra med buss-baserade system såsom i en processor. Om man lite grovt ska försökas förklara funktionen så har vi först och främst att när OE=1 och ingången är hög så leder T2. Därmed leder T3 och vi får låg signal ut. När insignalen är låg spärrar T2 och T3 varvid vi får hög signal ut. Om nu OE=0 kommer alla tre transistorerna att spärra och vi får hög impedans ut. Den allmänna symbolen är en triangel med en pinne (OE) på. Triangeln som finns med i figuren är ett annat sätt att rita en inverterare, vanligtvis av så kallad Schmitt-trigger typ.
Spikbildare


Spikar eller hasarder kan genereras på olika sätt beroende på vilken flanktyp man vill ska vara aktiv (detta används i flanktriggade vippor). Spikbildningen genereras på grund av den fördröjning (grindfördröjning) som alltid finns hos digitala kretsar. Bilden till vänster genererar således en spik då insignalen går hög. Detta för att NAND-grinden är hög när ingångarna är låga. Men när ingången sen går hög så tar det en pytteliten stund innan inverteraren (som här har gestaltats med hjälp av en NAND-grind med kortslutna ingångar) går låg. Under denna lilla stund är således båda ingångarna höga vilket får till följd att utgången blir kortvarigt låg. Denna spik är av storleksordningen nanosekunder och det kan hända att detta inte räcker för att till exempel nollställa en räknare. Man kan då prova att montera en liten kondensator på utgången av inverteraren för att ytterligare slöa ner den och därmed få en kraftigare spik. Alternativt kan man koppla flera (udda antal) inverterare i serie.
Vippapplikationer och realiseringar
I detta avsnitt behandlas en serie speciellt användbara minneselement eller så kallade vippor och hur de är realiserade och kan användas. Det finns fler vippor än de som gås igenom (bl.a JK-vippa) men de listade vipporna är de vanligaste. Den allra enklaste formen av vippa är SR-vippan.
Kontaktstudseliminerare (SR-Latch)

Ett par korskopplade NAND-grindar utgör en minnescell i form av en SR-vippa (observera att ingångarna är inverterade). Antag att SW står i läge nedåt. Q' kommer då garanterat vara hög (då NAND står för Not AND och alltså bara är låg när båda ingångarna är höga) och Q kommer att vara låg då båda dess ingångar är höga. När sedan SW byter läge kommer Q' genast gå låg samtidigt som Q går hög. När SW är i luften behålls nämligen det tidigare värdet (på grund av att S'R'=11) och tillståndsbytet sker bara en gång. Detta gör att kontaktstudsar elimineras.
Denna koppling är mycket effektiv när man vill koppla in brytare till processorer. Man slipper alltså filter och/eller speciella rutiner för att mjukvarumässigt filtrera en insignal. Nackdelen är att brytaren måste ha två lägen så det fungerar alltså inte med vanliga tryckknappar.
Flanktriggad D-vippa

En flanktriggad D-vippa (se spikbildare ovan) fungerar genom att varje gång klockpulsen CP (eng. Clock Pulse) går hög överförs värdet på ingången D till utgången Q. D-vippan består i grund och botten av en ännu enklare vippa. Om man tar bort inverteraren som går från D till den övre grinden och kallar den övre signalen för R (som i Reset) och byter ut D mot S (som i Set) får man nämligen en så kallad SR-vippa. Detta är den allra enklaste formen av (synkront) minneselement i digitala kretsar. 74HC74 är en flanktriggad (positiv flank) D-vippa.
D-vippa med asynkron Preset och Reset
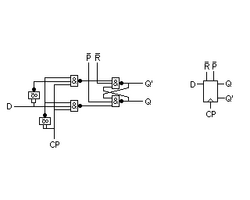
Med en flanktriggad D-vippa med asynkron Preset och Reset kan man godtyckligt tippa vippan åt endera hållet med hjälp av signalerna R' och P'. Dessa är aktivt låga och måste släppas höga innan nytt tillståndsbyte hos vippan kan ske.
SR-vippa

SR-vippan är en förenklad version av D-vippan. Dess sanningstabell visas till höger. Sanningstabellen skall tolkas som så att värdena i tabellen är de värden vippan antar som "nästa" värde, alltså vid nästkommande aktiv klockflank. Ingångsvärdet SR=11 är inte tillåtet (för då är vippan ej definierad).
D-vippa

D-vippan är en utvidgad version av SR-vippan. Dess sanningstabell visas till höger. Sanningstabellen skall tolkas som så att värdena i tabellen är de värden vippan antar som "nästa" värde, alltså vid nästkommande aktiv klockflank.
JK-vippa

JK-vippan är en utvidgad version av SR-vippan som involverar återkoppling. Dess sanningstabell visas till höger. Sanningstabellen skall tolkas som så att värdena i tabellen är de värden vippan antar som "nästa" värde, alltså vid nästkommande aktiv klockflank. JK-vippan har den fördelen över SR-vippan att den är definierad för alla typer av insignalskombinationer. Förutom att data togglar (dvs skiftar värde) för varje klockpuls när JK=11 så skiljer sig inte JK-vippan och SR-vippan sig åt. Det är exakt samma typ av minnescell.
T-vippa

T-vippan skiljer sig från frekvenshalveraren i det enda avseendet att togglandet är på och avstängningsbart med hjälp av styrsignalen T. Denna styrsignal består i sin tur egentligen av kortslutna ingångar hos en så kallad JK-vippa.
Frekvenshalverare

En frekvenshalverare är en vippa som byter tillstånd varje gång klockan (CP) går hög (eller låg beroende på flanktriggningen hos D-vippan vilken dock brukar vara positiv). Frekvenshalveraren är med andra ord en specialvariant av D-vippa där den inverterande utgången Q' har återkopplats till ingången. Detta får till följd att det krävs två flanker för att vippan ska gå från hög till låg, därav frekvenshalveringen.
Monostabil multivibrator

En monostabil (av mono, en) multivibrator har endast ett stabilt tillstånd. Eftersom kretsen ofta även har en inverterande utgång, Q', så är det svårt att säga vilket tillstånd som är det stabila men normalt brukar man säga att det normala tillståndet är låg medan det aktiva tillståndet är hög. Just denna krets triggas av negativ flank på B' varefter Q går hög under:
sekunder
vilket naturligtvis bara gäller för angiven krets men principen är densamma oavsett krets.
Astabil multivibrator

En astabil multivibrator med grindar kan konstrueras med tre olika typer av grindar (bara alla ingångar är ihopdragna). Dessa är NAND (Not AND), NOR (Not OR) eller inverterare.
Denna krets fungerar tyvärr endast med CMOS-kretsar ur exempelvis 74HC-serien eller 4000-serien. Detta för att drivning av TTL-ingångar kräver att den drivande enheten kan sänka ström (se TTL).
Man kan visa att frekvensen blir:
Multiplexer

I en multiplexer kan man med hjälp av styrsignalen ABC välja vilken av de åtta ingångarna som ska vara aktiv. Om styrsignalen ABC alltså till exempel är 110 binärt är ingång 6 aktiv osv. 74HC251 är en 8 Channel Multiplexer.
Avkodare

En avkodare (eng. demultiplexer) är uppbyggd kring ett antal AND-grindar och ett antal inverterare (representerade av ringarna). Avkodaren realiserar alltså alla tänkbara kombinationer av insignalen. Om ABC till exempel är 011 blir alltså AND-grind nummer 3 aktivt hög osv. 74HC138 är en 3-To-8 Line Decoder.
Omkodare

Omkodare, som ger binärkoden av insignalen ut, används inte så ofta. I en flash converter används de dock. Omkodaren har kunnat reducerats kraftigt i komplexitet med hjälp av Karnaughdiagram.
Insignalskombinationen x4x3x2x1=0000 får egentligen inte finnas då lägsta kod y2y1=00 avser indikera att x1 är hög. I praktiken har detta ingen betydelse för omkodaren får gärna lämna 00 ut oavsett om x1 är hög eller inte. Vilket den också gör då reduceringen gått så långt att x1 inte ens ingår i kombinatoriken.
Räknare
Asynkron räknare
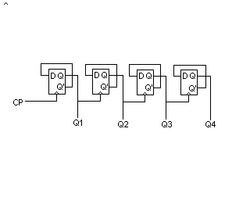
Den asynkrona binärräknaren kallas också ripple-carry-räknare. Enligt ovan vet vi att utgångarna växlar tillstånd varje gång CP går hög. Om man som i bilden kopplar utgångarna som klocka till nästkommande krets kommer varje utgång räkna binärt ett steg högerjusterat. Q1 räknar alltså minst signifikant och Q4 mest signifikant i just denna nibbel. 74HC191 är en 4-bit Binary Up/Down Counter.
Synkron räknare
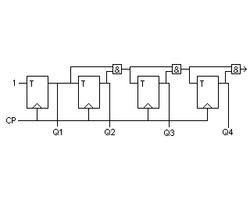
Till skillnad från den asynkrona räknaren ovan är denna räknare synkron med klockpulsen CP det vill säga den byter tillstånd exakt i takt med CP. Detta är en förutsättning för att räknaren ska kunna ingå i sekventiella nät såsom i en CPU. Räknaren utgörs av en serie T-vippor som fungerar som frekvenshalverare med tillägget att T måste vara hög för att tillståndsförändring skall kunna ske.
Programräknare (PC)

Programräknaren i en CPU ettställes vid spänningspåslag tack vare POR-kretsen vilket innebär att programräknaren (PC, från engelskans Program Counter) hoppar till resetvektorn på adress 1111 eller F hexadecimalt strax efter spänningspåslag och fortsätter räkna från den adress som PC då pekar på. Programräknaren måste alltså dels asynkront kunna, i det här fallet, ettställas dels kunna laddas med godtycklig adress (X1-X4). Programräknaren utnyttjar vippor med asynkron Preset (ettställning) och Reset (nollställning) ganska precist realiserad av den modifierade D-vippan ovan.
Ackumulator-komponenter
Ackumulator kallas den delen av en processor där resultat från ALU:n mellanlagras och manipuleras (främst skiftas eller jämförs). Multiplikation och division med multiplar om två är möjlig genom vänster respektive Högerskift.
Termen ackumulator betydde ursprungligen en enhet som kombinerade funktionen av tallagring och addition. Ett tal som överfördes till ackumulatorn adderades automatiskt med dess föregående värde. Räknarhjulsminnen hos tidiga mekaniska datorer hade ackumulatorer av denna typ.
Register

Det enklast tänkbara registret består bara av ett antal D-vippor.
Skiftregister

Detta skiftregister kan laddas parallellt och skicka data seriellt och det kan även laddas seriellt och skicka data parallellt. Vi närmar oss med andra ord en ackumulator.
Signalen Xin laddar vipporna parallellt med X1-X4, x är seriell data in och SV står för Skift Villkor och är aktivt hög för högerskift.
Ackumulator

Ackumulatorn består egentligen av två ackumulatorer (eller speciella skiftregister), för att skiftning ska kunna göras åt båda hållen. Data skyfflas alltså fram och tillbaks mellan Ackumulator A och Ackumulator B när skift åt olika håll måste göras. Data läggs då ut på databussen och på grund av att flera (interna) enheter delar på databussen så måste så kallade three-state buffrar (B1 och B2) användas. Dessa är alltså högimpediva när de inte används (EnA=EnB=0). Detta för att undvika kortslutning när andra enheter vill låna bussen. Insignalerna har bytt namn men torde vara lätta att identifiera om man jämför med skiftregistret ovan.
Komparatorer
Behovet att jämföra två tal är vanligt förekommande i all digitalteknik. Om vi antar att X=<x1, x2,...,xn> och Y=<y1, y2,...yn> är givna kan önskemålet antingen vara att indikera fallet X=Y eller att indikera något av fallen X>=Y, X>Y, X<=Y eller X<Y. Vi noterar att påståendet X>=Y är negationen till X<Y och om vidare variablerna permuteras övergår X>=Y i påståendet X<=Y och X<Y övergår i X>Y. Av detta resonemang framgår att man vid realisering av en komparator bara har att skilja på två fall:
och
Basic komparator

En basic komparator för xi=yi kan realiseras av en XOR-grind och en inverterare. Att det blir så enkelt är lätt att inse om man studerar sanningstabellen för en XOR-grind då den ju ger ett ut när signalerna är olika och således noll när signalerna är lika, därav inverteraren.
X=Y

I en komparator för X=Y genererar XOR-grinden, enligt ovan, hög signal ut om någon bitposition är olika. När man jämför hela tal räcker det alltså att kontrollera om någon XOR-grind har gått hög då detta indikerar olikhet. För man in den signalen på en OR-grind kommer den att gå hög så fort det är en olikhet i någon position och alltså indikera olikhet. Inverterar man sedan denna signal med hjälp av en inverterare (varvid man får en NOR-grind) kommer utsignalen alltså i stället indikera likhet dvs X=Y.
X<Y

Bilden visar en komparator för X<Y. Realiseringen skulle kunna vara borrow-kedjan i en subtraherare men vi har här valt en annan princip. Vi börjar alltså med den mest signifikanta positionen och konstaterar att om x1'y1=1 så gäller omedelbart att X<Y. Om dessutom w2=x1'+y1=1 (dvs de tre fallen x1y1=00, 01 eller 11) och x2'y2=1 har vi också X<Y. Wi=1 betyder alltså att även nästa position måste kollas om xi<yi eller ej.
ALU-komponenter
ALU står för Arithmetic Logic Unit och är den delen i en processor som utför aritmetiska beräkningar och då speciellt addition och subtraktion samt logiska operationer. Multiplikation och division sker normalt genom en serie additioner och subtraktioner. Ibland hårdkodas dock multiplicerare för att snabba upp processen (men vi är inte intresserade av snabba datorer här).
Basic adderare
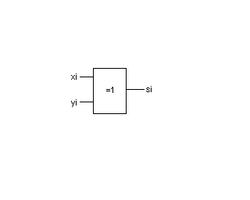
Bilden visar en basic adderare i form av en enda XOR-grind. En addition av två tal bestående av en bit vardera är alltså mer eller mindre komplett efter att ha passerat en XOR-grind. Två saker saknas dock. Det ena är genereringen av carry dvs ett slags overflow som inträffar när båda bitarna är höga (det som inom skolmatematiken kallas minnessiffra). Denna generering utförs av en halvadderare som är en basic-adderare med en AND-grind som jobbar på de ingående bitarna. Detta förstås lätt om man betänker att 1+1=0 med 1 som carry till nästa position. En heladderare tar även hänsyn till om det har genererats carry från föregående bitars addition och vidarebefordrar denna eventuella etta till nästa cell.
Heladderare (FA)

Bilden visar en heladderares bakomvarande teori och realisering. I a) visas hur minnesiffran kallad carry genereras både decimalt och binärt. En heladderare tar alltså hänsyn till om carry har genererats i högre position eller ej. I b) summeras helt enkelt carry med de båda bitarna xi och yi. Övriga kombinationer visas i sanningstabellen i c) varvid vi får Karnaughdiagrammen i d). Ur Karnaughdiagrammen får vi sedan:
och
vilket realiseras av grindarna i e). Den kompletta adderaren byggs sedan upp av en kedja av ovanstående struktur i f) kallade FA (från engelskans Full Adder).
Intresserade bör läsa artikeln adderare.
Helsubtraherare (FS)

Bilden visar en helsubtraherares bakomvarande teori och realisering. Talen antas positiva och representerade enligt
Y=<y1, y2,...,yn>
och
X=<x1, x2,...,xn>
där Y alltså subtraheras från X (D=X-Y).
I a) har vi använt den klassiska metoden med "lån" som markeras med ett streck över den siffra som är lånegivare. I de fall där närmast högre position i X är 0 fortplantar sig lånebehovet tills en 1:a påträffas som genom successiva lån överbringar en 2:a till den behövande positionen.
I b) har vi infört en ny rad för lånesiffrorna bi där bi=1 betyder lån från position i krävs av närmast lägre position i+1. För varje position ska vi sedan generera dels differenssiffran di dels eventuell borrow bi-1 (=lånekrav) till närmast högre position. Vid bildandet av differenssiffran gäller att xi har vikten +1, yi har vikten -1 och bi har vikten -1. Skulle det inträffa att denna summering blir <0 tar vi för givet att ett lån uttages av närmast högre position, dvs vi noterar bi-1=1 och underförstår samtidigt att aktuella positionen får ett tillskott av två.
Funktionstabellen får utseendet enligt c), Karnaughdiagrammet för di och bi-1 enligt d). Byggstenen i en subtraherare, i e) betecknad FS, kan alltså ges samma struktur som en heladderare (FA):
och
Funktionen di kan ges exakt samma form som summan si vid addition medan bi-1 överensstämmer med ci-1 om xi utbytes mot xi' (se respektive Karnaughdiagram).
En sak återstår: tolkningen av b0. Om X>=Y är uppenbarligen b0=0. Omvänt indikerar b0=1 att X<Y. Tyvärr är differensen D=<d1,d2,...,dn> i detta speciella fall inte en beloppsangivelse av |X-Y| som kanske vore önskvärt utan det så kallade 2-komplementet av differensens belopp. I de flesta datorer utförs därför inte subtraktion av en speciell subtraherare utan med en adderare och komplementerande nät. Detta möjliggörs genom representation av negativa tal med komplement.
Avancerad heladderare/helsubtraherare



Bilderna visar hur en heladderare/helsubtraherare (FA/FS) realiseras vid teckenbelopprepresentation.
Figur 1 visar alla in och utsignaler som en bitvis heladderare/helsubtraherare behöver. Dessutom visas ett par Karnaughdiagram som i grund och botten är sanningstabeller för signalerna (med den egenheten att signalernas möjliga tillstånd har sorterats så att mininering blir möjligt). Enligt Karnaughdiagrammet ska exempelvis utsignalen fi-1 både vara hög för xiyi=11 och hfi=00 samt för xiyi=11 och hfi=01. Med lite möda ser man att signalen fi inte behövs utan deluttrycket för fi-1 blir h'xiyi. I Karnaugdiagrammet är det dock enkelt att se då man kan para ihop ettorna.
Ettorna i Karnaughdiagrammen kommer alltså av att signalen (som står direkt under) skall vara hög vid de variabelkombinationerna. Vi kan titta på samma ettor som alltså säger att signalen fi-1 skall gå hög för xiyih'fi' respektive xiyih'fi. Vi har redan reducerat dessa uttryck men det är intressant att notera att FA/FS-cellen ska generera en carry (dvs fi-1) om xi är hög, yi är hög, h är låg (dvs addition) medan den ska strunta i fi. Detta är ju sant då 1+1 blir 0 med 1 som carry till nästa cell. På samma sätt fortsätter man sätta ettor i Karnaughdiagrammet (eller mer metodiskt i sanningstabellen som Karnaughdiagrammet avspeglar).
Med hjälp av Karnaughdiagrammen får vi:
och
Figur2 realiserar ovanstående med hjälp av XOR, AND och OR-grindar. Detta är alltså en FA/FS-cell som jobbar på enskild bit. Dessa kopplas i kedja för flera bitar.
Figur 3 visar en komplett realisering av en heladderare/helsubtraherare. När signalen SUB är låg är funktionen addition (x+y), subtraktion (x-y) när den är hög.
Det ska tilläggas för tydlighets skull att signalen h har följande logiska uttryck (se figur 3):
där x0 och y0 är teckenbitarna.
Från FA/FS går en något grövre ledare till XOR-grinden för realiseringen av differensen eller summan, |s|. Denna ledare representerar alla ingående bitar i talen.
Det finns också en signal benämnd eab vilket står för end around borrow. Vi ser genom att titta på kombinatoriken att denna signal genereras när f0 och h är ett dvs ett överskott av carry samtidigt som subtraktion ska ske.
Om f0 är hög samtidigt som en addition har skett, dvs h är låg, genereras spill (mer om det senare).
För en enklare beskrivning av adderare se adderare.
Permanentminne (ROM)
En CPU måste ha någon form av ett litet icke-flyktigt minne där den kan hämta basala instruktioner (instruktionsregister). Detta behöver dock inte vara programmerbart mer än en gång så man kan tänka sig att de små instruktionsprogrammen hårdkodas i det enklaste RISC-fallet, vilket vi i princip också gör nedan. Det vanligaste idag är annars EEPROM men för vår enkla CPU räcker nedanstående.
Basic permanentminne

Bilden visar ett basic permanentminne (ROM) realiserat med hjälp av AND och OR-grindar. X representerar den här tre bitar långa adressbussen. W indikerar vilket ord (egentligen ordledning) som är programmerat och b indikerar bitarna (egentligen bitledningar). På adress 010 (w2) är till exempel ordet 0110 programmerat. Detta blir alltså till data när adressen är 010.
Permanentminne i NAND-NAND struktur

Bilden visar ett permanentminne som man skulle kunna kalla MPROM (Mechanically Programmable Read Only Memory). Här används ju dioder i de positioner man vill ha höga och man skulle kunna tänka sig att dessa dioder mekaniskt kan flyttas runt i en "matrissockel". Det är även intressant att notera att då bitledningen i det här fallet är åtta bitar lång så innebär det 256 olika kombinationer. Här används alltså bara fyra. Man skulle dock kunna programmera fyra olika program samtidigt och sedan välja ett åt gången med hjälp av fyra multiplexrar. Alltså fyra olika program samtidigt och valbart i minnet. Dessa skulle alternativt kunna styras att väljas efter varandra och på så sätt utöka programlängden med en faktor fyra.
PLA

PLA står för Programmable Logic Array och är ett programmerbart permanentminne eller PROM. Programmeringen är väldigt enkel och utgörs av att diodfunktioner initieras både i AND-delen och i OR-delen. För väldigt små minnen, som i ett instruktionsregister, kan man programmera med hjälp av fysiska dioder enligt figur. Om man på detta sätt "hårdkodar" ett minne bör man dock komma ihåg dels att adressen måste finnas i inverterad form dels att utgången är något högimpediv och bör buffras.
CPU
En CPU (Central Processing Unit) är hjärnan i en dator.
Basic CPU

Bilden visar en enklast tänkbara maskin vilket skulle kunna representera en mycket enkel CPU där de interna instruktionerna (OP-koder) realiseras. Data ut skulle nämligen kunna användas kombinatoriskt och således styra upp vad som måste göras och i vilken ordning för att till exempel styra ackumulatorn till att realisera en sådan funktion som ROR (Rotate Right) dvs högerskift. Maskinen utnyttjar så kallat pageat minne med vilket menas att varje OP-kod eller instruktion får tilldelat sig en viss minnesarea som räknaren kan stega sig igenom. Detta för att räknaren stegar igenom de låga bitarna i adressen. Dock är det väl kanske att ta i och kalla detta för en CPU. Ett lämpligare namn vore instruktionsregister (IR).
Modern CPU

Bilden visar arkitekturen för en någorlunda modern CPU. Den innehåller alltså en enhet för aritmetiska och logiska operationer (ALU), en ackumulator (AC), en programräknare (PC), ett dataregister (DR), ett adressregister (AR), ett instruktionsregister (IR) och diverse kontrollsignaler (Control circuits).
Se även
Källor
- Per-Erik Danielsson, Lennart Bengtsson, Digital Teknik, tredje upplagan, 1986, Lund
- John P. Hayes, Computer Architecture and Organisation, Second Edition, 1988, Singapore
Externa länkar
 Wikimedia Commons har media som rör Digitalteknik.
Wikimedia Commons har media som rör Digitalteknik.
























